A Three-Layer Model

This post is part of a primer on infrared spectroscopy and global warming. The previous post introduces a two-layer model  and is a necessary prerequisite to understanding this post.  In this post I start with the following assumptions.  There is a source of infrared radiance that has emissivity of 1, i.e., it radiates as a perfect blackbody at a temperature of  288 K.  The radiance from that layer is I₀

There is a layer of air 1000 m thick with 380 ppm carbon dioxide at a temperature of 278 K.  There is another layer of air 1000 m thick with 380 ppm carbon dioxide at 268 K.  All layers are at a constant pressure of one atmosphere.

The equation to describe such a situation can be expressed as:

     I_s = I₂ + t₂(I₁-I₂) +t₁t₂(I₀-I₁)

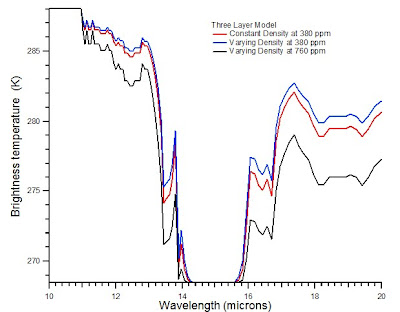
where  t₁and t₂ each represent the transmittance of the corresponding layer, and I₁ and I₂ represent the radiance from a blackbody at the temperature of the given layer.  The results are shown in the plot of brightness temperature versus wavelength at the top of this post.

Rationalizing the Expression

Note that in the case where t₂ = 1that this expression becomes equivalent to the two-layer model.  The expression uses the same logic:

The two-layer model yielded the expression:

     I_s = I₁ + t₁(I₀-I₁)

Now, consider only the additional layer, layer 2.  Let that radiance impinging on layer 2 be I_s1, then according to the two-layer model the radiance that exits layer 2 is:

     I_s = I₂ + t₂(I_S1-I₂)

I_S1 is can also be equated with the radiance that exits layer 1 to impinge on layer 2:

     I_s1 = I₁ + t₁(I₀-I₁)

Substitution for I_s1 yields the three-layer model:

     I_s = I₂ + t₂(I₁ + t₁(I₀-I₁)-I₂)
    
The Significance

As altitude increases through the troposphere, in general each layer is cooler than the previous layer.  Where the transmittance is equal or nearly equal to 1, radiation from lower levels is transmitted through a given layer.  If the transmittance is equal to or nearly equal 0, i.e., the transition is saturated in that region, the layer emits radiation equivalent to a blackbody at the temperature of the layer.  Intermediate values of the transmittance lead to intermediate radiance from the layer.  Not that this effect is amplified by adding more layers.  In the two-layer model,  the carbon dioxide spectrum in the region greater than 15 microns appeared to be nearly saturated.  In the three-layer model , the region of apparent saturation is smaller.

Here one can begin to see that increasing the level of carbon dioxide in the atmosphere will lead to more absorption of radiation at higher levels of the troposphere.  There is more to the story, however.

Density Effects

As altitude increases through the troposphere, the density of gases decreases.  The ratio of carbon dioxide concentration in parts-per-million by volume does not change as the density decreases, but if I had chosen to use units of milligrams per meter cubed (mg/m³), the concentration would decrease the density of the atmosphere.  There are advantages and disadvantages to either choice of units, but the point is that there are fewer absorbers in a given volume as one increases the altitude.  So even where the absorption is saturated it will be less so at higher altitudes.  If one uses units of ppm, the change in density can be considered a change in the absorptivity, or if one uses density units in the Beer's Law expression, no adjustment is necessary.

Consider now a three-layer system in which the density of the upper layer is 80% of the air density at one atmosphere.  For fun, I also calculate what happens if the concentration of carbon dioxide is doubled. The plot below shows the original three-layer model, as well as a three-layer model in which layers 1 and 2 have different densities at 380 and 760 ppm.

This model should not be taken too seriously as it is still overly simplistic.  Notice, however, that increasing the level of carbon dioxide significantly increases the absorption of radiant energy.  If one so desired, one could build up successive discrete layers of the atmosphere to build a four-layer model, a five-layer model and so on.  As temperature and pressure actually vary continuously, there are obvious limitations to using a finite number of discrete layers.

Absorptivity Changes

Throughout this exercise I have assumed that the absorptivity itself is not a function of temperature or density.  In fact, both temperature and density have effects on the absorptivity function that become more pronounced at lower densities and temperatures such as those found in the upper troposphere.

At lower temperatures, the ground state rotational distribution of the vibrational transition is colder.  The population in states of higher rotational quantum number is decreased, and thus these transitions fade out as the temperature gets colder at higher altitudes.  Additionally, there is a broadening of rotational lines with increased temperature that owes to Doppler broadening. This effect narrows the lines as altitude increases.

As the density decreases, the frequency of collisions between molecules also decreases and this effect also narrows the lines as altitude increases.

Emissivity of the Earth


This analysis treats the source of radiance as a blackbody at 288 K, but the earth is not a black body, and the emissivity of the earth must be taken into account as part of the zeroth layer. 

Other Species

In this exercise I have neglected other absorbing species chief among them water and ozone that also absorb infrared radiation.  These other species have overlapping absorptions that must be included in a full radiative transfer model.

Reflectance, Aerosols, and Mie Scattering

The model so far has neglected the role of reflectance as well as the presence of aerosols in the atmosphere that can scatter infrared radiation.  Water and dust aerosols play a significant role in the atmosphere and these must be included in modeling the atmosphere.

Toward a Radiative-Transfer Model of the Atmosphere

Even the simple model described here required the use of a computer to keep track of the different spectral channels.  In principle, a model this simple could be worked out by hand, if one were willing to carry out the hundreds of calculations necessary to account for each spectral channel.  It should be obvious that as the model becomes more realistic, and hence more complicated that the use of computers to do the modeling becomes absolutely essential.

Criticizing a model because it requires a computer and software is an absolute cop-out.  One often hears criticism of atmospheric models on the basis of the fact that the models are complex and require computers.  In truth, one ought to criticize models that are not complicated because they are too simplistic.

It is perfectly fair to criticize complicated models of the atmosphere, but that criticism must have some basis to it.  One cannot fairly criticize a model that one does not understand.  If one understands the model, criticizes it and suggests improvements, one has started to do real science.  Criticisms of models made by people who do not understand them should not be taken seriously at all.  One must demonstrate some level of understanding to earn the right to have one's criticisms taken seriously.

In this series of posts I have been inching toward describing a radiative transfer model of the atmosphere.  It is my sincere hope that anyone who has read this far, now has a somewhat better understanding of what such a model entails.  Before going further, however, it is necessary to have some understanding of the structure of the atmosphere.

The next post looks at that structure.

Sources

• Alison K. Lazarevich, Christopher C. Carter, Michael E. Thomas, Isaac N. Bankman, Eric W. Rogala, and Richard J. Green,  Determination of CL Using Passive Remote Sensing of  Background Radiance, Sixth Joint Conference on Standoff Detection for Chemical and Biological Defense, 25-29 October 2004, Williamsburg, VA
• Chandrasekhar, S., 1950. Radiative Transfer, Oxford University Press, London (reprinted by Dover New York).
• Dry Adiabatic Lapse Rate
• NIST Webbook
• Air Density and Density Altitude