Molecules and Radiation II: Molecular Vibration, Rotation, and Translation

This post is part of a primer on infrared spectroscopy and global warming. The previous post  starts the process of looking at the interaction between infrared radiation and molecules and discusses the degrees of freedom of molecules and the Born-Oppenheimer approximation.  The result of the previous post is that for the purposes of IR spectroscopy, one can focus on the motion of the atomic nuclei and separate them from the electronic degrees of freedom of a molecule.

Figure Source

There are 3N nuclear degrees of freedom for a molecule that has N nuclei.  For the HCl molecule that means there are 6 degrees of freedom.

Three of those degrees of freedom involve translation of the molecule in three dimensions.  This translation causes broadening of spectral peaks because of the Doppler effect, but the existence of absorption does not arise because of these degrees of freedom.  I briefly discuss this effect, and then I dispense with translation.

Briefly, consider a source of infrared radiation that is stationary relative to an observer.  Now consider that molecules are in motion relative to this stationary source.  Because the speed of light does not change in the frame of reference of the absorbers, the frequency of the radiation must be different.  Because molecules are moving in all directions, some will see a frequency higher than the observer sees and some will see a frequency lower than the observer sees.  This effect broadens line shapes and is called Doppler broadening.

The degrees of freedom are now reduced to 3N - 3, or for HCl 3 degrees of freedom.

Molecules that are not linear can rotate on three axes. Linear molecules can only rotate on two axes.  This fact might be confusing at first, but consider that the degrees of freedom I am discussing all arose from x, y, and z translations of the nuclei.  There is no combination of these translations that results in a linear molecule spinning on its linear axis.

When I first started discussing the degrees of freedom, I explicitly neglected spin of the particles involved.  Nuclear spin can have a projection along the linear axis.  Additionally electron angular momentum, and electron spin can have projections along this axis.  In counting only two degrees of rotational freedom for a linear molecule, I am neglecting these considerations.

These rotational degrees of freedom are important for vibrational spectroscopy because rotational structure is superimposed on top of vibrational structure and is evident in vibrational spectra. For the moment, note that rotation will show up in vibrational spectra, but I need to address vibrational spectra first.

The remaining degrees of freedom are vibrational modes.  For a linear molecule, there are 3N - 5 vibrational modes.  Other molecules have 3N - 6 vibrational modes.  HCl is a linear molecule; so it has one vibrational mode.  This may seem trivial, the vibration is simply the displacement of the HCl bond away from its equilibrium position, but note that in more complex molecules that these formulas can be helpful in counting the vibrational modes.

Consider some of the atmospheric gases of interest. N₂ is a linear molecule with two nuclei: it has one degree of vibrational freedom.  O₂  is a linear molecule with two nuclei: it also has one degree of vibrational freedom.  These two molecules are not IR absorbers.  Why that is true is discussed in the next post, but they do vibrate just as HCl does.

CO₂ and N₂O are linear molecules with three nuclei. They have 9 - 5 = 4 vibrational degrees of freedom.  H₂O, and O₃ are bent molecules with three nuclei each. They each have 9 - 6 = 3 vibrational degrees of freedom.

CO₂ has 4 vibrational degrees of freedom, two of which are degenerate.

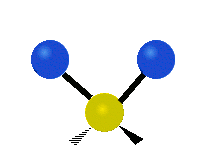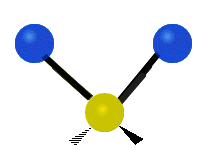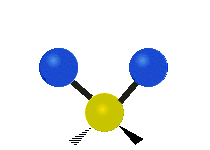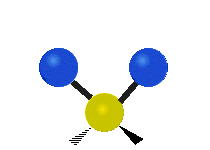
The first is a symmetric stretch (a) , in which both  carbon oxygen bonds synchronously lengthen and shorten from their equilibrium bond lengths.    The second (b) is an asymmetric stretch, in which both carbon oxygen bonds are stretching, but not symmetrically.

The third and fourth modes, are degenerate bending modes. For example (c), in which the molecule is bending in the plane of this blog, and another mode in which the bend is our of the plane.

N₂O has the same modes as CO₂, except that the "symmetric" stretch is not really symmetric because one bond is a nitrogen-nitrogen bond, and the other is a nitrogen-oxygen bond.A nice illustration of nitrous oxide vibrations can be found here. 

Water and ozone are bent molecules. They have three vibrational modes.  Water is a very complicated molecule.  There are features in its IR spectrum that require going a little deeper than a simple vibrational mode analysis.  Keeping that in mind, one must start somewhere.  Water has three modes, a symmetric stretch, and asymmetric stretch and a bending mode. Ozone also has a symmetric stretch, an asymmetric stretch, and a bending mode.

The next post in this series looks more in depth at vibrational modes and how they give rise to infrared spectra. 

Sources

• Wikipedia: "Infrared Spectroscopy"
• N2O Vibrations 
• Water Absorption Spectrum