Dipole Transition Moment
In previous posts in this series I hinted at the fact that there has to be an interaction between the radiation and the molecule for it to absorb radiation. Consider the HCl molecule. Because the chlorine nucleus has a stronger tendency to attract electrons than the hydrogen nucleus (see electronegativity), the electrons are shared unequally. This unequal sharing results in a partial negative charge on the chlorine nucleus and a partial positive charge on the hydrogen nucleus. As the HCl molecule vibrates, the distance between the partial positive and partial negative charge oscillates. That is to say that HCl has a dipole moment that changes as a function of its molecular vibration. This feature is precisely what is necessary to interact with electric dipole radiation. From this fact, one predicts that HCl will absorb radiation of the proper frequency.
There is a more mathematically formal way of saying the same thing. I do not want to delve into the details, but I want to at least mention it so that if it appears in other contexts, readers can connect it to this idea. You can skip the next little bit, if it makes no sense to you.
Let Ψi be the molecular wavefunction in the initial quantum state of the molecule. Let Ψf be the molecular wavefunction in the final quantum state of the molecule, and let μe be the electric dipole moment operator. The transition dipole moment expression can be written as:
<Ψf|μe|Ψi>
The condition for a transition is that this expression is non-zero.
78% of the dry atmosphere is made up of nitrogen (N2) gas. 21% of the dry atmosphere is made out of oxygen (O2). Both of these molecules are called homonuclear diatomics. They are molecules composed of two atoms that are the same. Other examples of homonuclear diatomics include hydrogen (H2), fluorine (F2), and chlorine (Cl2). Because both atoms are the same, they attract electrons equally. As electrons are shared equally, there is no net charge on either atom. Homonuclear diatomics do not have a permanent dipole moment. As they vibrate, the dipole moment remains zero. Therefore, the vibrational mode does not interact with electric dipole radiation.
99% of the dry atmosphere is transparent to IR. The greenhouse effect only exists because of trace gases in the atmosphere. So when someone says that because the concentration of carbon dioxide is only 380 ppm (0.038%) and cannot have a big effect on the planet, that person is either repeating a talking point without understanding it or being deliberately deceptive. Without the greenhouse effect, the earth would be uninhabitable. Water vapor is the most significant greenhouse gas, and it is the reason that the earth has a temperate climate.
Carbon dioxide (CO2) is a linear triatomic molecule. Electrons are shared unequally resulting in a partial positive charge on the carbon and a partial negative charge on the oxygen atoms. Because carbon is the central atom and the molecule is linear, it has two equal and opposite dipole moments that cancel. This means that carbon dioxide does not have a permanent dipole moment.
 Figure Source
Figure SourceFrom the previous post carbon dioxide has 3(3) - 5 = 4 vibrational modes. The first of these modes is the symmetric stretch, in which the both carbon oxygen bonds are stretching in phase. In this mode, the dipole moment does not change because the carbon oxygen distances are always equal and the dipole moments along each bond remain equal and opposite. So the symmetric stretch vibration of carbon dioxide is not dipole allowed.
Carbon dioxide has three other modes, an asymmetric stretch and two degenerate bending modes. All three of these modes are dipole allowed. In the asymmetric stretch the bond lengths are no longer equal, and the dipole moments are no longer equal and opposite. This results in a net change in dipole moment as the carbon dioxide molecule stretches asymmetrically. In the bending modes the oxygen atoms move in a scissoring motion breaking the linear symmetry and resulting in a change of dipole moment with the vibration.
Nitrous oxide is also a linear triatomic molecule, but this time a nitrogen is in the center with a nitrogen on one side and an oxygen on the other side. Because the atoms on each side of the central atom are different, nitrous oxide has a permanent dipole moment. It has two different stretch modes, and two degenerate bending modes, all of which are IR active.
Water vapor (H2O) is the most important greenhouse gas. Water is a bent molecule with a partial negative charge on the oxygen and partial positive charge on the hydrogen atoms. It has a permanent dipole moment because it is bent. Also, because it is bent, it has only 3 vibrational modes, a symmetric stretch, an asymmetric stretch and a bend. All three modes are IR active.
Ozone (O3) plays a variety of roles in the atmosphere. It is probably most famous for the fact that it absorbs ultraviolet (UV) radiation. This absorption involves the electronic degrees of freedom. In addition to being an important UV absorber, ozone is also an important IR absorber. Ozone is a bent molecule. For reasons having to do with its electronic structure, electrons are sheared unequally with the central atom being charged positively and the the other atoms having negative charge. Ozone has a permanent dipole moment, and all three vibrational modes are electric dipole allowed.
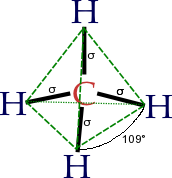
Methane (CH4) is another important greenhouse gas. It is the first molecule considered here that is not planar. Methane has a tetrahedral geometry that one must visualize in three dimensions.
Methane does not have a permanent dipole moment. This fact may be hard to visualize. Although carbon-hydrogen bonds are usually considered non-polar, there is a slight polarity to the bond with the hydrogen atom being slightly positively charged. Pick two carbon-hydrogen bonds and imagine the average of the dipole moment vectors. It is halfway between the two vectors. Now pick the other two bonds and imagine the average between their dipole moment vectors. The two averaged vectors are equal and opposite so that methane does not have a permanent dipole moment. This may be difficult to visualize and it does not matter so much as the conclusion is understandable.
Methane has 3(5) - 6 = 9 vibrational modes. They are not easy to visualize. There is a symmetric stretch mode that is not IR active. A doubly degenerate mode that is not IR active, and two triply degenerate modes that are IR active.
There are other gases that make up the atmosphere and many of their modes can be found here.
Classical Harmonic Oscillator
A harmonic oscillator is a system that oscillates about its equilibrium position with a linear restoring force. For a classical harmonic oscillator, consider a spring. The harder that it is compressed, the harder it pushes back. The longer it it is stretched the more it pulls back. Of course, real life springs are not perfectly harmonic oscillators, but one has to understand the basic expression before fixing it. The same is true for molecular vibrations. The expression for a spring with a linear restoring force is known as Hooke's Law:
F = -kx
in which F is the restoring force, x is the displacement from equilibrium (choosing x=0 as the equilibrium position) and k is the spring constant. Newton's Second Law of motion states that F = ma = m (d2x/dt2) so the expression becomes:
m (d2x/dt2) = -kx
There are an infinite number of solutions to this equation, one of which is:
x = A sin ((k/m)1/2 t)
in which A is the amplitude of the motion (how far the spring is compressed or stretched). For convenience, let ω = (k/m)1/2:
x = A sin (ωt)
Because the sin function is periodic with a frequency of 2π, the frequency, ν = ω/2π. ω is called the angular frequency. In a perfect harmonic oscillator, the energy is constant; it is exchanged between kinetic and potential energy. At the equilibrium position, the spring is moving fast and all the energy is kinetic. As it compresses or stretches to an extreme, that energy is converted to potential energy in the form of tension of the spring. At the most extreme deviation from equilibrium, all of the energy. At any point in time the potential energy of the oscillator is:
V = kx2/2
Quantum Harmonic Oscillator
The solution of the Shrödinger equation for a harmonic oscillator yields a wavefunction whose energy levels are given by:
Ev = ħω (v + 1/2)
H-bar, ħ, is Planck's constant divided by 2π,and Ev is the energy of the wavefunction with quantum number v. Notice that the lowest energy level, v= 0, has residual energy, called the zero-point energy. This fact can be understood by the Uncertainty Principle. A harmonic oscillator with no energy would be at its equilibrium position and have a momentum of zero. If that were the case, its position and momentum could be determined simultaneously with arbitrary accuracy.
[Figure of a Harmonic Potential-needs to be replaced- RJG 10/17/11]
Most molecular vibrations can be treated as harmonic oscillators to a first approximation. This approximation breaks down eventually for all molecular vibrations. For example, for a high enough quantum number the vibration has enough kinetic energy to overcome the restoring force and break the bond. Deviations from the harmonic approximation can be treated by adding anharmonic (i.e., higher order) terms to the equation. There are also other potential functions, such as the Morse potential that can be used. The harmonic approximation is helpful to understand features of vibration in molecules, but ultimately, the energy levels can be ascertained from empirical data from IR spectroscopy.
Selection Rules
In the section on the dipole transition moment, I state that a condition for a molecule to absorb or emit IR is that the dipole transition moment is non-zero:
<Ψf|μe|Ψi> ≠ 0
Often, when evaluated for combinations of initial and final state this expression becomes zero and no transition is formally allowed. Within the harmonic approximation only states with v = ±1 are allowed. This fact does not mean that other transitions cannot be observed in real molecules. The harmonic approximation breaks down and often overtone vibrational transitions can be observed, but in general they are not as strong as the harmonically allowed transitions.
Resonance
The other condition for absorption or emission is resonance. The photon energy being absorbed or emitted must equal the energy difference of the two vibrational states. For example for a transition from v = 0 to v = 1, the energy of the photon being absorbed, Eph, must satisfy:
Eph = E1 - E0
where Eph = hν
Population Distributions
In a sample of gas phase molecules, the energy levels of those molecules are distributed. For a transition to occur from a given vibrational energy level, there must be molecules that are in that energy level. Allowed transitions from vibrational energy levels that have a higher population are more easily observed than transitions from energy levels that have lower populations. In the HCl molecule the energy difference between v=0 and v=1 is 2885.9 cm-1. Treating HCl as a two-level system, it is possible to calculate the population in v=1 from the Maxwell-Boltzmann distribution.
N1/ N0 = exp (-2885.9 cm-1/kT)
where N is the population in the given level, k is Boltzmann's constant and T is the temperature in Kelvin. It is necessary to do some bookkeeping with units. A useful number to know is that at 300 K, the factor kT = 208.57 cm-1. So
N1/ N0 = exp (-2885.9/208.57) = exp(-13.84) = 9.758 x 10-7
In words, about 1 molecule in a million is in v = 1 at room temperature.That means that the HCl IR spectrum should be dominated by the vibrational transition from v=0 to v=1.
HCl Vibrational Spectrum
The HCl spectrum can be found here. The NIST website allows you view the spectrum in wavenumbers or microns and in absorbance or in transmittance. Another post in this series discusses the difference between absorbance and transmittance.
Notice the clump of lines distributed about 2885.9 cm-1. These lines arise from vibrational transition from v=0 to v=1.
Ro-Vibrational States
Notice that there is more than one line and that there is no line at exactly at 2885.9 cm-1. These line arise from changes in rotational state, J, that occur at the same time as the vibrational transition. The rotational selection rules for HCl are that the change in rotational quantum number, J, must be ±1 for the dipole transition moment to be non-zero.
The part of the spectrum in which J increases by one is called the R-branch. In this branch transition requires more energy than the vibrational transition, and so the branch lies at higher wavenumber than a vibrational transition with no rotational change would lie.
The part of the spectrum at lower energy, corresponding to transitions, in which, J decreases by one is called the P-branch.
The term Q-branch refers to transitions in which J does not change. If it were an allowed vibrational transition in HCl , it would appear at 2885.9 cm-1.
Each line in the spectrum corresponds to a transition from an individual rotational state, J, in the vibrational ground state to the next higher or lower J-state in the excited vibrational state. Those with very good eyes may notice that these lines are split. The splitting originates from the fact that Cl has two natural isotopes 35 and 37. The difference in mass affects the rotational energy levels.
The next post in this series looks at infrared spectra of several molecules of importance in understanding climate.
Sources
- Wallace, John M., Atmospheric Science, Elsevier, Amsterdam, 2nd Edition, 2006
- Struve, Walter S., Fundamentals of Molecular Spectroscopy, John Wiley & Sons, New York, 1989
- Steinfeld, Jeffrey I, Molecules and Radiation, The MIT Press, Cambridge, MA, 2nd edition, 1985
- Atkins, P. W. Physical Chemistry, New York: W. H. Freeman and Company, New York, 3rd edition, 1986
- Nitrous Oxide Vibrations
- HITRAN vibrational modes
- McQuarrie, Donald A., Statistical Thermodynamics, University Science Books, Mill Valley, CA, 1973
- NIST web book
- Isotopes of Chlorine




1 comment:
Post a Comment